Calculateur de Segment

Cet outil est un Calculateur et grapheur d'un segment. Parmi les caractéristiques calculées : longueur, pente, milieu, vecteur normal, équation de la droite du segment et équation de la médiatrice.
Calcul des équations paramétrique, vectorielle et explicite du segment.

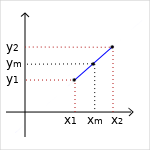
Formules de calcul dans un segment de droite

On note :
S : un segment du plan (ce dernier est muni d'un repère orthonormé (O,X,Y))
(x₁ , y₁) : coordonnées du point de départ du segment S
(x₂ , y₂) : coordonnées du point d'arrivée du segment S

Longueur du segment

`L = sqrt((x_2-x_1)^2+(y_2-y_1)^2)`

Pente du segment

La pente du segment S est définie quand `x_2 != x_1` (segment non vertical)

`m = (y_2-y_1)/(x_2-x_1)`

Equation explicite du segment

On suppose que `x_2 != x_1` (autrement dit, le segment S n'est pas vertical)

Soient m et p tels que,
m est la pente du segment S définie ci-dessus,
`p = y_1 - m*x_1`

alors l'équation explicite du segment S s'écrit comme suit :

`y = mx+p , x in [x_1,x_2]`

(on suppose que `x_1 < x_2` sinon remplacer `[x_1,x_2]` par `[x_2,x_1]`)

Equation vectorielle du segment

Le segment S est composé des points M tels que :
`\vec(OM) = \vecu + t \vecv \text{ } t in [0,1]` ,
`\vecu = ( x_1 , y_1 )`
`\vecv = ( x_2-x_1 , y_2-y_1 )`

Equation paramétrique du segment

Cette équation découle de la forme vectorielle. Un point M de coordonnées (x , y) appartient au segment S, si et seulement si,

`x = x_1 + t*(x_2-x_1)`
`y = y_1 + t*(y_2-y_1)`
`t in [0,1]`

Milieu du segment

Le milieu du segment S a pour coordonnées,
`x_m = (x_1+x_2)/2`
`y_m = (y_1+y_2)/2`

Equation de la médiatrice du segment

On suppose que :
* `y_2 != y_1` et `x_2 != x_1` (c'est à dire que le segment S n'est ni horizontal ni vertical)
* m : pente du segment S (définie ci-dessus)
* (`x_m` , `y_m`) : coordonnées du milieu du segment S (définies ci-dessus).

alors l'équation de la médiatrice s'écrit comme suit :

y = n.x + q

avec n et q, la pente et l'ordonnée à l'origine de la médiatrice,
n = -1/m
`q = y_m - n*x_m`

Vecteur normal du segment

Le vecteur normal `\vecn` du segment S est le vecteur orthogonal au vecteur dont les extrémités sont les points de départ et le point d'arrivée du segment S. Ainsi, le vecteur normal est donné par:

`\vecn` : (`y_1-y_2` , `x_2-x_1`)

Voir aussi

Calculateur de droite
Calculateur de vecteur
Calculateurs de Géometrie analytique
Calculateurs de Géometrie
Calculateurs mathématiques