Calculateur de deux vecteurs
Produit scalaire
Soient `\vecu` et `\vecv` deux vecteurs de l'espace euclidien de dimension 3, `\mathbb{R^3}`, ayant les coordonnées suivantes :
`\vecu = (x_1,x_2,x_3)`
`\vecv = (y_1,y_2,y_3)`
alors le produit scalaire de `\vecu` par `\vecv` s'écrit,
`\vecu . \vecv = x_1.y_1 + x_2.y_2 + x_3.y_3`
Il existe une autre définition du produit scalaire utilisant la norme vectorielle et l'angle `\theta` formé par les vecteurs `\vecu` et `\vecv` :
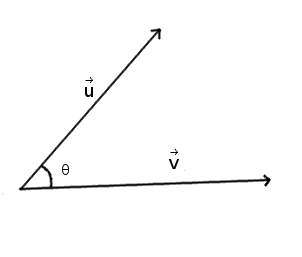
Le produit scalaire est égal à :
`\vecu . \vecv = norm(u) . norm(v) . cos(\theta)`
Au passage, on peut déduire la formule de calcul de l'angle entre 2 vecteurs :
`\theta = arccos((\vecu . \vecv) / (norm(u) . norm(v)))`
Exemple:
Soient `\vecu` et `\vecv` deux vecteurs ayant les coordonnées suivantes dans un repère orthonormé:
`\vecu = (1,4,-3)`
`\vecv = (10,2,2)`
alors le produit scalaire de `\vecu` par `\vecv` s'écrit,
`\vecu . \vecv = 1.10 + 4.2 + (-3).2 = 12`
Projection vectorielle
La projection vectorielle d'un vecteur `\vecu` sur un vecteur non nul `\vecv` est la projection orthogonale de `\vecu` sur `\vecv` comme indiqué sur le schéma ci-dessous (`\vecu_1` étant la projection de `\vecu` sur `\vecv`).
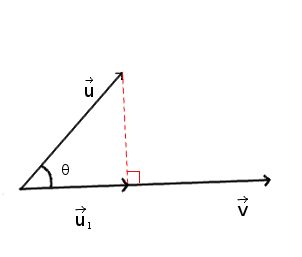
`\vecu_1` est défini par:
`proj_\vecv(\vecu) = \vecu_1 = \(vecu . \vecv)/norm(vecv)^2 . \vecv`
Une autre formule:
On peut aussi utiliser l'angle `\theta` formé par les vecteurs `\vecu` et `\vecv`. La projection de `\vecu` sur `\vecv` peut être définie comme suit :
`\vecu_1 = proj_\vecv(\vecu) = (norm(vecu).cos(\theta)) . \vecv / norm(v)`