Lens maker equation

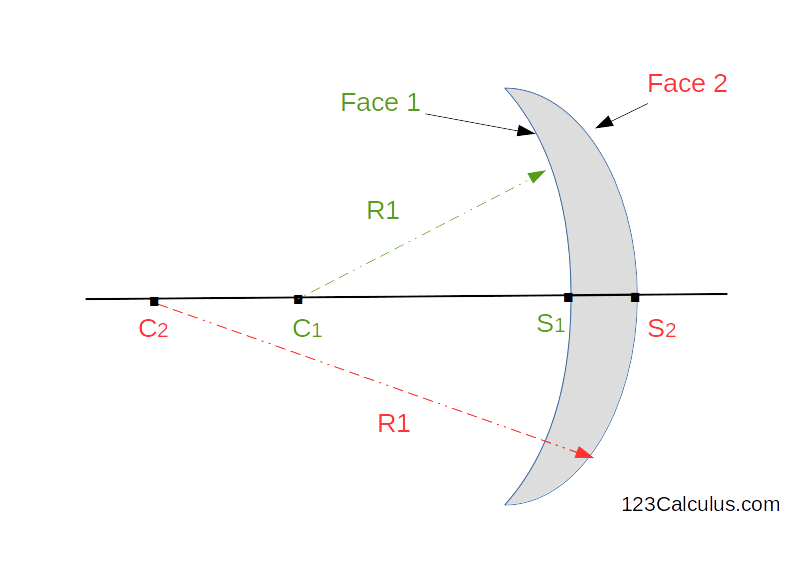
Diagram: Example of a converging meniscus lens composed of two spherical diopters of radius `R_1` and `R_2`.

The lens maker equation computes the focal length of a lens, from the radii of curvature of the two spherical diopters that compose it (face 1 and 2 in the diagram) and n, the refractive index of the lens material. The optical power of the lens can be easily deduced using the formula `f = 1 / V` (See Calculate the optical power of a lens.)

When projected on the plane, the lens has two sides (see diagram above):
- Face 1: circle of center `C_1` and radius `R_1`
- Face 2: circle of center `C_2` and radius `R_2`

It is assumed that the lens is thin ie its thickness e is small relative to the radii of curvature `R_1` and `R_2` (e << `R_1` and e << `R_2`). The lens focal length is given by the lens maker formula :

`1/f = (n-1)*(1/R_1-1/R_2)`

`R_1`: Radius of curvature of the first surface.
`R_2`: Radius of curvature of the second surface.
`n`: Lens material refractive index
`f`: Lens focal length

If one of the faces of the lens is plane then the radius is infinity (`R = oo`). The formula remains valid, just omit the corresponding term: `1/R = 0`. In the calculator, simply enter a large number like 1e10 m as radius (= `10^10` m).

Sign convention

The radii of curvature `R_1` and `R_2` may be positive or negative depending on the shape of the surfaces of the diopters constituting the lens.

Directional distances :
`R_1 = \bar{S_1C_1}`
`R_2 = \bar{S_2C_2}`

So,
- `R_1 > 0` if `S_1` is convex
- `R_1 < 0` if `S_1` is concave
- `R_2 > 0` if `S_2` is concave
- `R_2 < 0` if `S_2` is convex

See also

Calculate the vergence of a lens
Two circles Calculator
Optics calculators