Thin Lens Formula
Thin lens formula or Gaussian Lens formula.
Enter 'x' in the field to be calculated.
This tool is a thin lens formula calculator. It computes the image position of an object through a thin lens. All distances are measured from the center of the lens and obey a sign convention (see below).
To compute the position of the object by taking the lens focal points as origins, use this version Newton's version of thin lens equation.
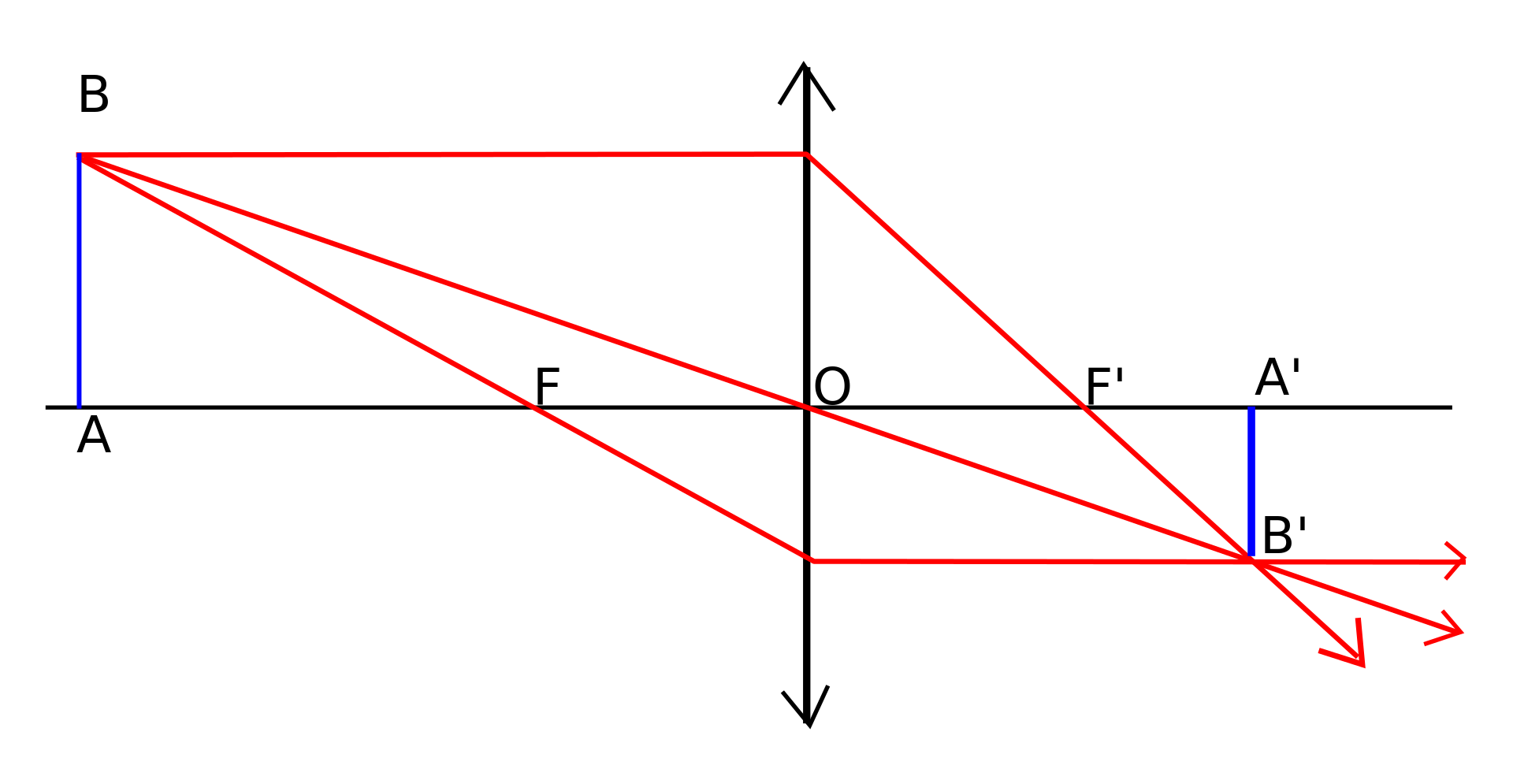
d0 : distance from object to lens in cm (directional distance AO in the diagram)
d1 : distance from lens to image in cm (directional distance OA' in the diagram)
f : focal length in cm (OF' in the diagram)
All these distances obey the sign convention below.
Sign convention :
- All distances are measured in relation to the lens surface.
- The direction of light from object to lens is considered as the 'positive direction' (always from left to right).
- The focal length is positive (f > 0) for a converging lens and negative (f < 0) for a diverging lens.
The thin lens formula is then expressed as follows,
`1/d_0 + 1/d_1 = 1/f`
Calculation example : case of a converging lens
The purpose is to calculate the position of the image of an object which is 20 cm away from a converging lens. We suppose that the lens focal length is 5 cm. So we have,
- Object distance: d0 = 20 cm (directional distance from object to lens).
- Focal length: f = 5 cm (positive for a converging lens)
We get (enter "x" in d1 field),
d1 = 6.67 cm
The image is a real image (ie can be viewed on a screen) located 6.67 cm to the right of the lens.
Case of a diverging lens
Under the same conditions as above (converging lens case) but with a diverging lens, we have,
- Object distance : d0 = 20 cm.
- Focal length : f = -5 cm (negative sign for a diverging lens)
We get (enter "x" in d1 field),
d1 = -4 cm
The image is a virtual image (can not be seen on a screen) located 4 cm to the left of the lens.
See also
Newton conjugation relationship
Lens optical power
Optics Calculators