Two vectors calculator
Dot product
If `\vecu` and `\vecv` are two vectors in the 3-dimensional space `\mathbb{R^3}` with the following coordinates :
`\vecu = (x_1,x_2,x_3)`
`\vecv = (y_1,y_2,y_3)`
then the dot product of `\vecu` by `\vecv` ca be written,
`\vecu . \vecv = x_1.y_1 + x_2.y_2 + x_3.y_3`
There is another definition using the vector norm and the angle `\theta` formed by vectors `\vecu` and `\vecv`:
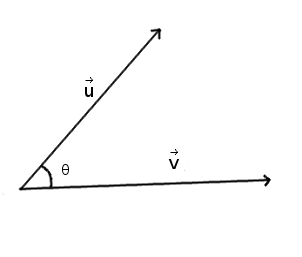
The dot product is then calculated as follows,
`\vecu . \vecv = norm(u) . norm(v) . cos(\theta)`
By the way, we can calculate the angle between the two vectors with the following formula,
`\theta = arccos((\vecu . \vecv) / (norm(u) . norm(v)))`
Example:`\vecu` and `\vecv` are two vectors with the following coordinates :
`\vecu = (1,4,-3)`
`\vecv = (10,2,2)`
then the dot product of `\vecu` by `\vecv` is,
`\vecu . \vecv = 1.10 + 4.2 + (-3).2 = 12`
Vector Projection
The vector projection of a vector `\vecu` on a non-zero vector `\vecv` is the orthogonal projection of `\vecu` to `\vecv` as shown in the diagram below (`\vecu_1` being the projection of `\vecu` on `\vecv`).
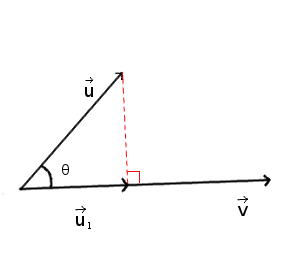
`\vecu_1` is defined by:
`proj_\vecv(\vecu) = \vecu_1 = \(vecu . \vecv)/norm(vecv)^2 . \vecv`
Another formula:
The angle `\theta` formed by the vectors `\vecu` and `\vecv` can also be used. The projection of `\vecu` to `\vecv` can be defined as follows:
`\vecu_1 = proj_\vecv(\vecu) = (norm(vecu).cos(\theta)) . \vecv / norm(v)`