Equation de l'opticien

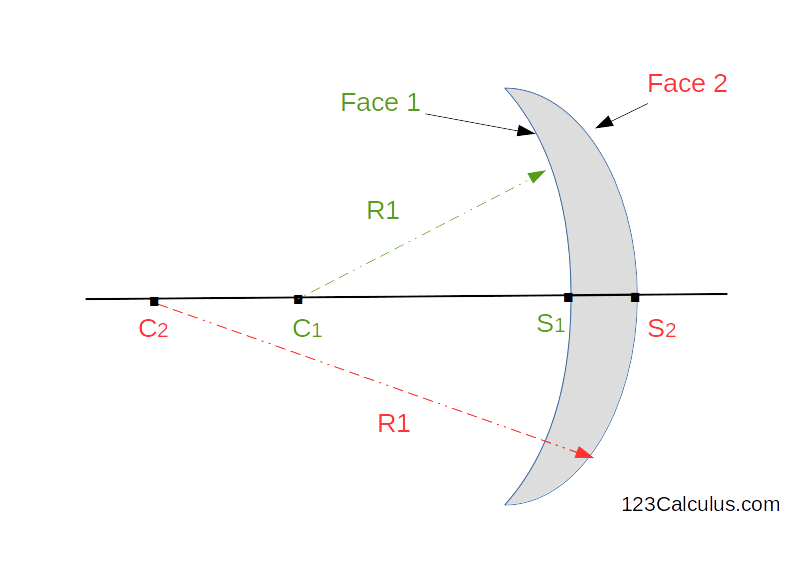
Schéma : Exemple d'une lentille de type ménisque convergent formée de deux dioptres sphériques (faces) de rayons `R_1` et `R_2`.

L'équation de l'opticien calcule la distance focale d'une lentille en fonction des courbures des deux dioptres sphériques qui la constituent (face 1 et 2 dans le schéma) et de l'indice n du matériau de la lentille. La vergence de la lentille peut être aisément déduite à l'aide la formule `f' = 1 / V` (Cf Calculer la vergence d'une lentille.)

Projetée sur le plan, la lentille a deux faces (schéma ci-dessus) :
- Face 1 : cercle de centre `C_1` et de rayon `R_1`
- Face 2 : cercle de centre `C_2` et de rayon `R_2`

On suppose que la lentille est mince c'est à dire que son épaisseur e est faible par rapport aux rayons de courbures `R_1` et `R_2` (e << `R_1` et e << `R_2`). La distance focale peut être calculée comme suit :

`1/f = (n-1)*(1/R_1-1/R_2)`

`R_1` : Rayon de courbure de la première surface rencontré par la lumière.
`R_2` : Rayon de courbure de la deuxième surface rencontré par la lumière.
`n` : Indice de réfraction du matériau de la lentille
`f` : distance focale de la lentille

Si l'une des faces de la lentille est plane alors le rayon est infini (`R = oo`). La formule reste valable il suffit d'omettre le terme correspondant : `1/R = 0`. Dans le calculateur, il suffit de saisir un grand nombre dans le champ 'rayon' comme 1e10 m (= `10^10` m).

Convention de signe

Les rayons de courbure `R_1` et `R_2` peuvent être positifs ou négatifs selon la forme des surfaces des dioptres constituants la lentille.

Ecriture algébrique:
`R_1 = \bar{S_1C_1}`
`R_2 = \bar{S_2C_2}`

Cela revient à,
- `R_1 > 0` si `S_1` est convexe
- `R_1 < 0` si `S_1` est concave
- `R_2 > 0` si `S_2` est concave
- `R_2 < 0` si `S_2` est convexe

Voir aussi

Calculer la vergence d'une lentille
Calculateur de deux cercles
Calculateurs optiques