Loi de la réfraction
Loi de la réfraction dite loi de Snell-Descartes.
Saisir 'x' dans le champ à calculer.
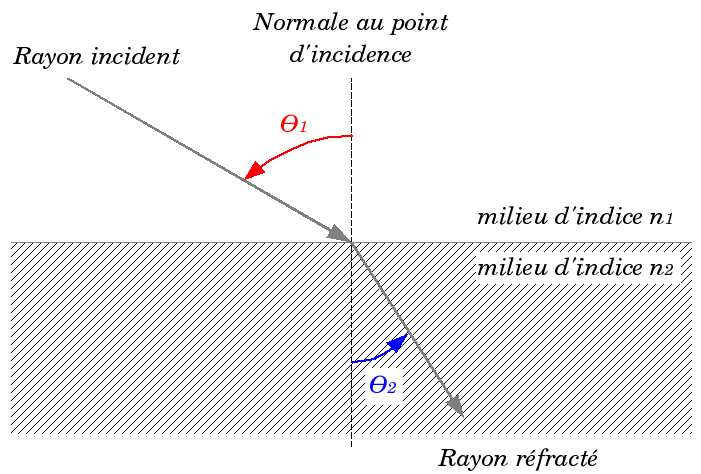
Ce calculateur exprime la loi de la réfraction ou la loi de Snell-Descartes :
`n_2*sin(theta_2) = n_1*sin(theta_1)`
n1 : indice de réfraction du milieu 1 (celui du rayon incident)
n2 : indice de réfraction du milieu 2 (celui du rayon réfracté)
`theta_1` : angle d'incidence
`theta_2` : angle de réfraction
Cette loi décrit le comportement de la lumière lorsqu'elle change de milieu. Plus précisément, elle permet de calculer l'angle de déviation de la lumière suite au passage d'un milieu d'indice de réfraction n1 vers un autre milieu d'indice de réfraction n2. On appelle cet angle "l'angle de réfraction".
Réfraction et réfringence
La réfringence d'un milieu est sa capacité à réfracter les rayons de la lumière.
Or, L'angle de réfraction dépend du rapport entre les deux indices de réfraction n1 et n2 car,
`sin(theta_2) = (n_1/n_2)*sin(theta_1)`
En conséquence,
- si n2 > n1 : le rayon de lumière passe à un milieu plus réfringent, alors,
`sin(theta_2) < sin(theta_1)`
donc le rayon lumineux va se rapprocher plus de la normale (`theta_2 < theta_1`). C'est le cas dans le schéma ci-dessus.
- A contrario, si n2 < n1 : le rayon de lumière passe à un milieu moins réfringent, alors,
`sin(theta_2) > sin(theta_1)`
donc le rayon lumineux va s'éloigner plus de la normale (`theta_2 > theta_1`).Angle critique de réfraction
`sin(theta_2) = (n_1/n_2)*sin(theta_1)`
Or `sin(theta_2) <= 1` donc,
`(n_1/n_2)*sin(theta_1) <= 1`
`sin(theta_1) <= n_2/n_1`
Cette égalité est toujours vérifiée quand `n_2 > n_1`.
Mais pour n1 > n2, il est mathématiquement possible de trouver des valeurs de `theta_1` telle que cette inégalité n'est pas vérifiée ! Dans ce cas, si on saisit ces valeurs dans le calculateur alors ce dernier va afficher la valeur NaN comme valeur de `theta_2` (cad indéfinie).
Dans ce cas, il n'y a pas réfraction mais une réflexion totale du rayon lumineux qui ne traverse pas le milieu 2.
L'angle limite `theta_1` auquel cela arrive s'appelle l'angle critique de réfraction et se calcule comme suit,
`(n_1/n_2)*sin(theta_1) = 1`
`theta_1 = Arcsin(n_2/n_1)`
En résumé, on constate que si n2 > n1 (passage à un milieu plus réfringent) alors, le rayon de lumière va toujours être réfracté en se rapprochant de la normale.
Si n2 < n1 (passage à un milieu moins réfringent) alors, le rayon de lumière va être réfracté en s'éloignant de la normale à condition que l'angle d'incidence ne dépasse pas une limite (angle critique de réfraction calculé ci-dessus). Au delà de cette limite, le rayon lumineux va être totalement réfléchi (le milieu 2 va agir comme un miroir!).