Relation de conjugaison de Descartes
Loi de Descartes ou relation de conjugaison avec origine au centre.
Saisir 'x' dans le champ à calculer.
Cet outil est un calculateur de la relation de conjugaison de Descartes.
La loi de Descartes, applicable pour tout système optique obéissant aux conditions de Gauss, permet dans la pratique de calculer la position de l'image d'un objet à travers un système optique comme une lentille mince, un dioptre sphérique, etc.
Nous l'appliquons dans ce qui suit à une lentille mince.
Pour calculer la position de l'objet en prenant comme origine les foyers de la lentille, utiliser plutôt cette version : relation de conjugaison de Newton.
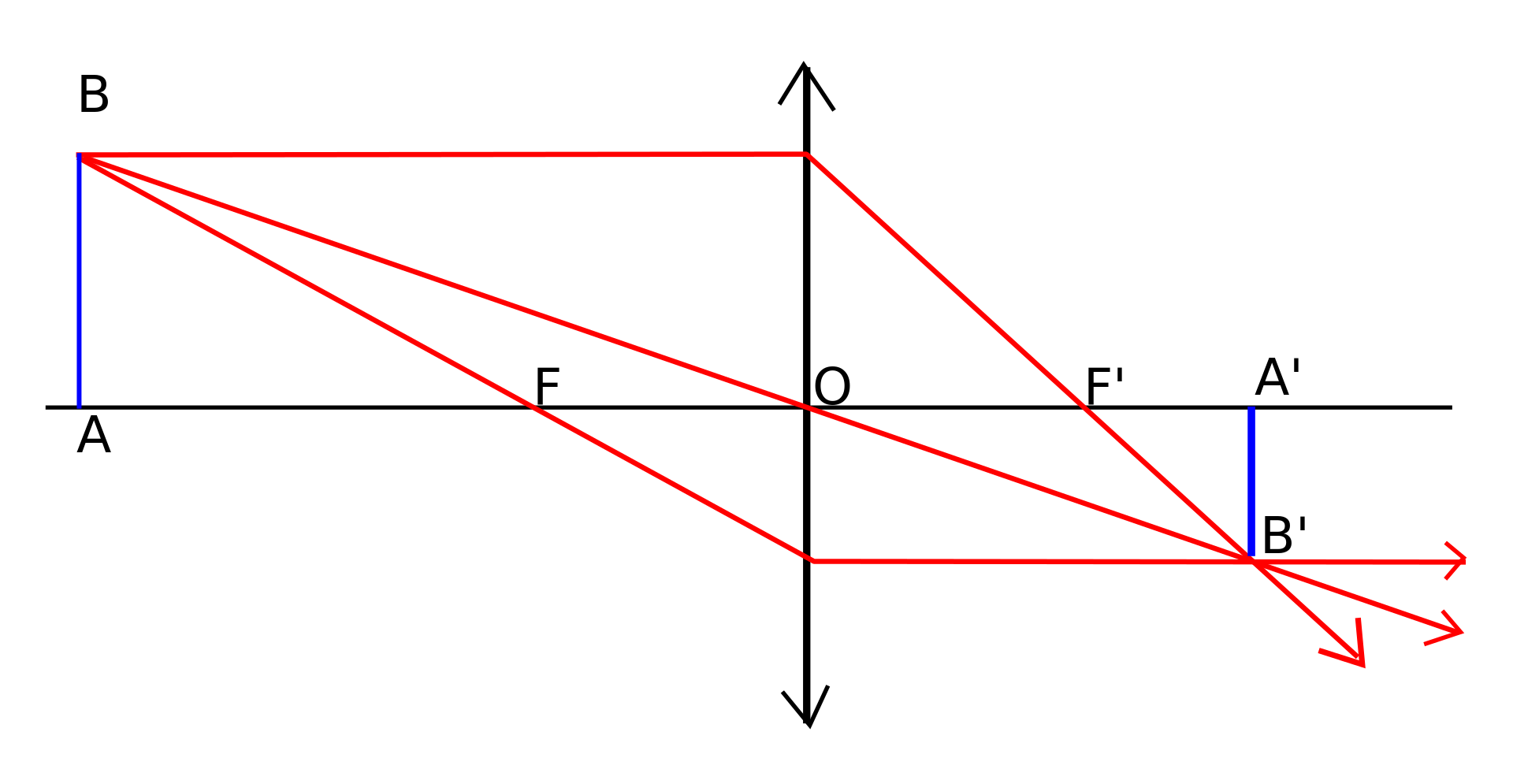
Convention pour les signes : le sens de la propagation de la lumière est pris comme le sens positif. Dans le schéma, le sens de la lumière va de gauche à droite (de l'objet vers la lentille) donc `\bar{OA} < 0` et `\bar{OA'} > 0`.
`\bar{OA}` : distance algébrique centre de la lentille - objet (en m)`\bar{OA'}` : distance algébrique centre de la lentille - image (en m)
`f'` : distance focale image (en m)
V : vergence de la lentille (en dioptries)
La loi de Descartes ou relation de conjugaison s'exprime alors ainsi,
`1/\bar{OA'} - 1/\bar{OA} = 1/{f'} = V`
Attention : bien faire attention aux signes des différents paramètres !
Rappel: le sens de la lumière est pris comme le sens positif.
Dans le schéma (cas d'une lentille convergente), on a,
- Distance objet : `\bar{OA} < 0`
Ceci est vrai en général car l'objet est généralement situé à gauche de la lentille et la lumière se dirige toujours de l'objet vers la lentille.
- Distance image : `\bar{OA'} > 0`
- Distance focale image : `\bar{OF'} = f'` on a, `f' > 0`
- Vergence : `V > 0`
Calcul de la position de l'image : lentille convergente
Il s'agit de calculer la position de l'image d'un objet situé à 20 cm d'une lentille convergente de 5 cm de distance focale image. Avec les notations du schéma, on a,
- Distance objet : `\bar{OA} = -20 cm`
- Distance focale image : `\bar{OF'} = 5 cm`, ce qui équivaut à une vergence V = 1/0.05 = 20 `\delta` (dioptries)
On obtient avec le calculateur (en saisissant "x" dans le champ OA'),
OA' = 6.67 cm
L'image obtenue est une image réelle (ie peut être visible sur un écran) située à droite de la lentille à 6.67 cm du centre de la lentille.
Calcul de la position de l'image : lentille divergente
On reprend les mêmes conditions mais cette fois avec une lentille divergente.
Il s'agit de calculer la position de l'image d'un objet situé à 5 cm d'une lentille divergente de 20 cm de distance focale image. On a,
- Distance objet : `\bar{OA} = -5 cm`
- Distance focale image : `\bar{OF'} = -20 cm`, ce qui équivaut à une vergence V = -1/0.2 = -5 `\delta` (dioptries)
On obtient avec le calculateur (en saisissant "x" dans le champ OA'),
OA' = -4 cm
L'image obtenue est une image virtuelle (ie qu'on ne peut pas voir sur un écran) située à gauche de la lentille à 4 cm de la lentille.
Voir aussi
Relation de conjugaison de Newton
Calculer la vergence d'une lentille
Calculateurs optiques